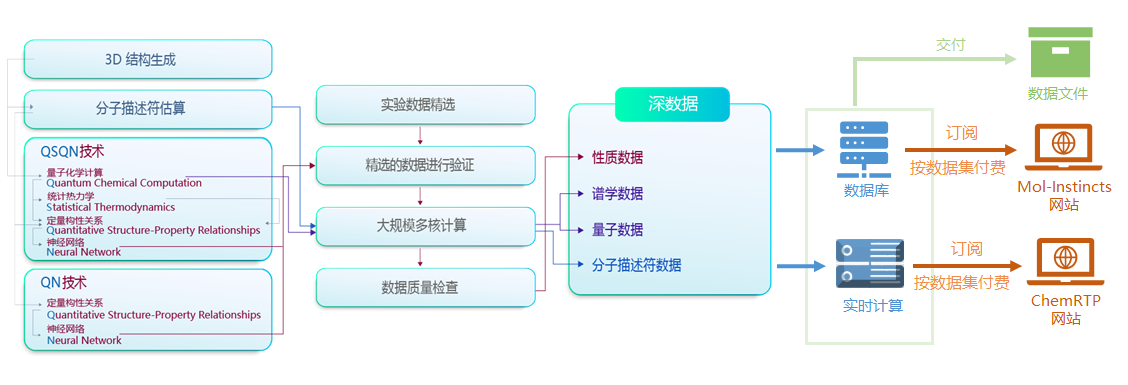
几分钟内生成数百万个3D结构
利用结构生成引擎来生成化合物的3D结构。基于用户输入的公式(原子及其数目)和/或核心结构(应该包含的结构),结构生成引擎自动生成所有可能的异构体,如下图所示:

例如,输入C22H46时没有指定核心结构,则在几分钟内总共会生成2278658个结构。如果在同分异构体列表中存在对映异构体,结构生成引擎会自动过滤掉它们,因为它们的深数据值是完全相同的。
生成化合物深数据的41项专利的核心技术称为“QSQN技术”,本技术基于量子化学(Quantum
chemistry)、统计热力学(Statistical
thermodynamics)、QSPR(定量构性关系)和神经网络(Neural network)的组合,并结合几乎所有可用的实验数据的系统分析。
首先生成化合物的3D结构并估算2D分子描述符,然后用生成的3D结构数据及3D分子描述符估算进行高质量的量子化学计算,之后根据量子计算结果采用统计热力学方法。再从分子描述符估算、量子计算和统计热力学应用相组合的信息应用于QSPR建模,最后应用神经网络模型对QSPR建模结果进行更新。QN技术包含2D
QSPR和神经网络(Neural network),不包含量子计算,QN技术能够实时生成部分性质数据。技术组件和组合过程的概述如下所示。
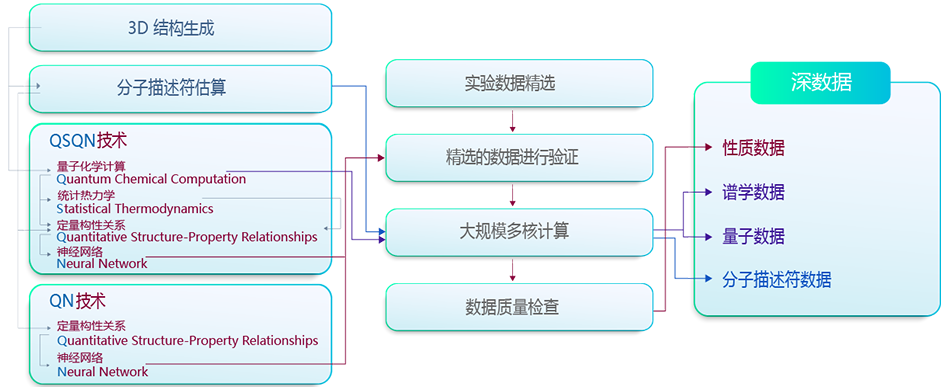
QSQN和QN都能生成热物理化学、热力学、传递和/或药物性质数据,这些数据列在深数据列表页面的性质数据部分。生成的性质数据用实测的性质数据进行了验证,这些数以百万计的实验数据是前期收集和完善的。通过大规模的多核计算自动生成大量的深数据。这些性质数据通过系统的质量检查以确保其准确性和一致性。
谱学数据和量子数据作为性质数据生成的副产品,是由量子化学计算及大规模的多核计算产生的。类似地,分子描述符数据是由分子描述符估算和大规模的多核计算产生的。下面给出了每个过程的进一步描述。
利用结构生成引擎来生成化合物的3D结构。基于用户输入的公式(原子及其数目)和/或核心结构(应该包含的结构),结构生成引擎自动生成所有可能的异构体,如下图所示:

例如,输入C22H46时没有指定核心结构,则在几分钟内总共会生成2278658个结构。如果在同分异构体列表中存在对映异构体,结构生成引擎会自动过滤掉它们,因为它们的深数据值是完全相同的。
利用3D结构生成引擎生成的结构,2D分子描述符根据其定义1估算。每个化合物估算了2,000多个描述符,分为24类,如下所示:

一些高质量的描述符(如分子轨道能量、静电描述符等)需要量子化学计算(包括优化的3D结构)支持。基于量子化学计算值可以得到可靠的3D分子描述符,如下所述。
量子化学计算能否获得可靠的优化结构极大程度决定于几何优化的初始结构。在进行量子计算之前,详细的构象分析可以确保获得 一个"良好"的初始结构。如果结构中存在一个或多个单键,进行构象分析则可由结构生成引擎生成3D结构。根据单键的数量,可以自动生成多达数百个构象。随后,基于Halgren2提出的MMFF94s力场,就可以对每个构象进行简单的势能计算。然后势能最低的构象就作为几何优化的初始结构。
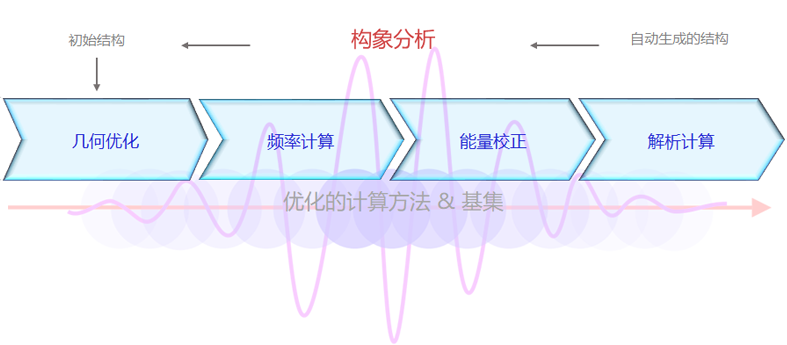
在确定计算方法(如Hartree-Fock、密度泛函理论等)和基集(如STO-3G、6-31G*等)的最优组合之前,尝试了2000多次的系统研究,用于预测热物理化学、热力学、传递和/或药物性质数据。通过对实验的熵、偶极矩、频率、热容、磁化率、极化率、回转半径、范德华面积和范德华体积的预测精度分析,得出对于含C、H、N、O和S化合物,6-31G*基集的DFT-B3LYP泛函数3及C - pVDZ基集的RI-MP2能量校正为最优组合。最优组合的精度高、计算时间合理。对于不含C、H、N、O、S原子的化合物,没有能量校正的3-21G*基集的B3LYP方法是最优组合。
B3LYP计算用于获得化合物的与性质数据相关的基本信息。进行了包含受阻转子校正和能量校正的几何优化和频率计算,对无虚频的最小值生成的优化结构进行了仔细验证,解析计算得到了谱学数据。
确保尽可能多的可靠实验数据点以建立可靠计算模型只管重要。在5年多的时间里,我们从超过16万个不同的来源(包括期刊文章、科学书籍和专利)收集了超过23万个化合物的150多万种性质数据点。
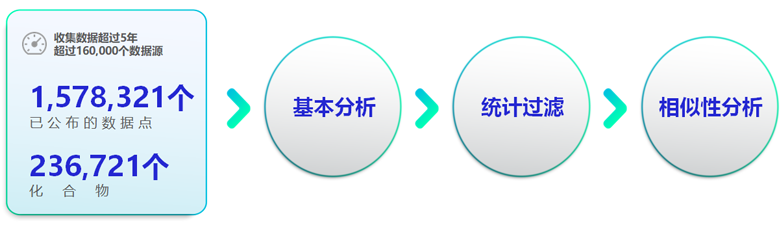
实验数据可能有很大误差,因此在使用它们建模之前进行了系统性地筛选,以确保数据点可靠。数据精选程序包括基本分析、统计过滤和相似性分析。以常沸点为例,对这些方法有详细描述。查看数据精选细节
对超出实验点范围的数据做可靠预测是开发计算模型的最终目标之一,因为基于没有科学原理和/或物理意义的经验性的公式和/或参数的计算模型往往不可用。而基于科学原理的模型其预测可靠性通常会显著的提高,但是这需要更多的知识、洞察力和努力。
统计热力学作为机理建模的基础可以提供性质数据的可靠预测。例如,理想气体热容的数学表达式如下:
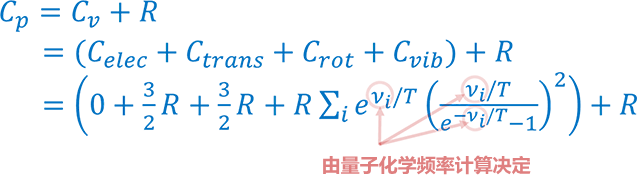
平动和旋转贡献是气体常数(R)的三分之二,振动贡献是根据量子化学频率计算(包括受阻转子修正)得到的振动频率值(ni)确定的。
我们发现,基于量子化学数据和统计热力学的模型通常可以出色的预测性质数据的趋势、特征和/或行为。然而,统计热力学并不能提供所有热物理化学、热力学、传递和/或药物的性质的数学公式,这些性质在深数据列表页面的性质数据部分列出。绝对预测精度也不总是满足要求,这已经通过使用QSPR和神经网络模型得到了改善,如下面的章节所述。当统计热力学不能提供数学公式时,也可以使用QSPR和神经网络方法。
QSPR建模已经用于深数据列表页面的性质数据部分中的各种性质了。利用筛选的实验数据和可用的统计热力学结果能从24个类别的2000多个描述符中为QSPR建模选择自变量。实验数据按3:2或7:3的比例分成训练集和测试集,以便对QSPR模型中的参数进行适当的估算。
最初,使用正向加法和反向消除的逐步法估算,该方法提供了所需描述符的简短扫描,以使平方相关系数(R2)和统计f检验达到可接受水平。为了执行统计上有意义的逐步选择,至少需要数量级为100的自由度。由于有大量的收集和筛选好的可用的实验数据,确保了可以达到1,000至10,000数量级的自由度。换句话说,每种性质的QSPR建模中涉及的化合物数量的数量级在1,000到10,000之间。每两个描述符之间的相互关联系数都经过仔细检查,以确保所选描述符具有足够的独立性。多元线性回归的参数估计只有在t值具有统计显著性时才是有意义的。
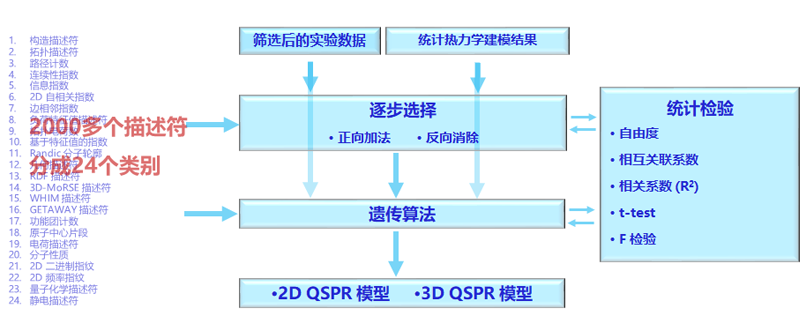
一旦逐步选择成功,获得的描述符信息就作为超参数输入到遗传算法中,并执行更高级的搜索。用超参数再次搜索整个描述符空间,以确定描述符的最佳组合。在遗传算法步骤中,描述符、统计t值、平方相关系数和统计f值之间的相互关联系数再次被仔细检查。如果全部满足要求,QSPR建模完成。
QSPR模型从仅含C和/或H原子的化合物逐步进行。然后,化合物扩展到包括C、H、N、O和/或S原子,最后扩展到包括C、H、N、O、S、F、Cl、Br、I、Si、P和/或As原子。2D和3DQSPR模型都进行了建设。经过数年的多次尝试,所有的模型开发都非常成功。在大多数情况下,平方相关系数大于0.95,统计检验完全满足要求。
由于2DQSPR模型不需要量子化学描述符,因此计算速度非常快,几乎可以实时获得性质数据。然而,2D QSPR模型的精度和可靠性普遍低于3D QSPR模型。3D QSPR模型通常具有更高的精度和可靠性,但需要比2D QSPR模型大得多的计算量。
QSPR建模假定要预测的性质和所选择的描述符之间存在线性关系,但这并不反映非线性关系是否存在。如果非线性存在并将其引入,采用神经网络建模可以改善模型。
实验数据以3:1:1或7:1.5:1.5的比例分成训练集、验证集和测试集,用于神经网络模型的开发。输入层中的节点由QSPR模型的结果自动确定,这些结果与QSPR模型的描述符完全相同。输出层中有一个单独节点,就是要预测的性质。
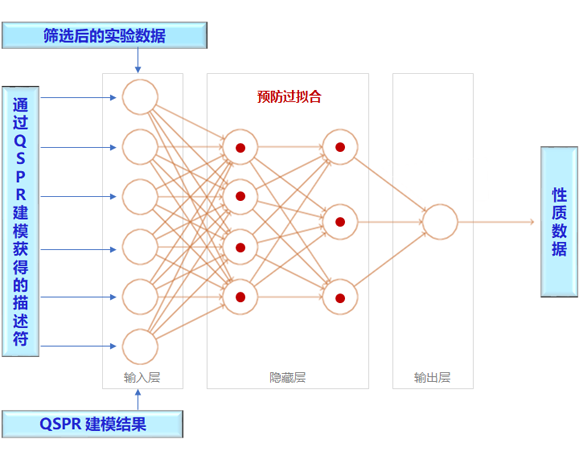
要谨慎对待以最小化神经网络建模中典型的过拟合问题。利用实验数据集和QSPR建模结果进行交叉验证,对过拟合进行检测。一旦检测到,就通过减少隐藏层的数量、隐藏层中的节点数量和/或节点的一定权重来防止过拟合。
大量试验表明,隐藏层的数量需要为1,并且在大多数情况下,隐藏层中的节点数量需要至少低于输入层中的结点数量,以防止过拟合。与QSPR模型的R2值相比,最终的神经网络模型的R2值提高了约7%。
使用最终的计算模型,预测并验证了与所有筛选的实验数据点相对应的性质数据点。
在常数性质中,最初对奇偶校验图和预测数据的分布作为与实验数据的偏差百分比的函数进行了验证。以常沸点为例如下所示。
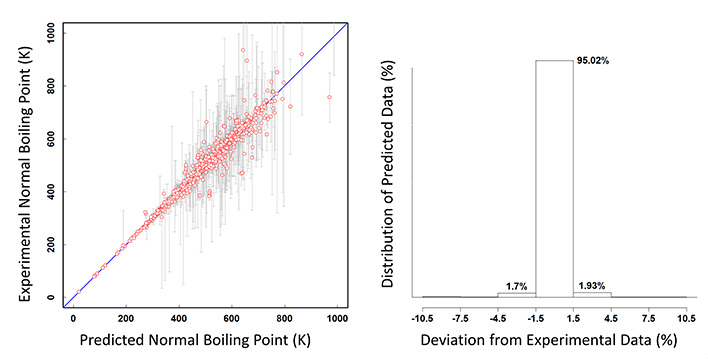
左侧的奇偶校验图也通过垂直灰线显示了多个实验数据的范围。预测数据的分布表明,95%以上的预测点与筛选的实验数据的偏差在1.5%以内。
筛选的实验数据和预测数据之间还进行了点对点的对比。举例说明,对于100个选定的样本化合物的常沸点,下面给出了最终QSQN模型的预测数据与筛选的实验数据之间的点对点对比表。
| NO | Chemical Compound Name (Click to View Structure) |
Formula | Experimental Data | QSQN Model Predicted | ||
|---|---|---|---|---|---|---|
| Minimum | Refined | Maximum | ||||
| 1 | (1R,4S)-bicyclo[2.2.1]hept-2-ene | C7H10 | 365.0 | 369.1 | 372.9 | 368.967 |
| 2 | (2E)-but-2-en-2-ylbenzene | C10H12 | 461.5 | 467.3 | 472.6 | 467.269 |
| 3 | (2E)-hex-2-ene | C6H12 | 337.6 | 341.1 | 344.5 | 341.241 |
| 4 | (2R)-1,1,2-trimethylcyclohexane | C9H18 | 414.2 | 418.3 | 422.5 | 418.476 |
| 5 | (2R)-2-(ethylsulfanyl)butane | C6H14S | 402.8 | 406.9 | 410.9 | 406.570 |
| 6 | (2R)-2-methylthiolane | C5H10S | 401.1 | 406.0 | 411.3 | 405.954 |
| 7 | (2R)-butan-2-yl pentanoate | C9H18O2 | 443.2 | 447.6 | 452.1 | 447.476 |
| 8 | (2S)-2-methylhexanal | C7H14O | 410.1 | 415.1 | 420.2 | 414.908 |
| 9 | (2S,5S)-5-ethyl-2-methylpiperidine | C8H17N | 432.2 | 436.6 | 441.0 | 436.273 |
| 10 | (2Z)-hex-2-ene | C6H12 | 338.6 | 342.1 | 345.5 | 342.059 |
| 11 | (3E)-hex-3-ene | C6H12 | 336.8 | 340.3 | 343.8 | 340.439 |
| 12 | (3R)-2,3,4,4-tetramethylhexane | C10H22 | 430.4 | 435.1 | 439.8 | 435.300 |
| 13 | (3R)-3-methyldodecane | C13H28 | 498.5 | 503.5 | 508.6 | 503.627 |
| 14 | (3R)-3-methylpentadecane | C16H34 | 549.5 | 555.0 | 560.6 | 555.096 |
| 15 | (3R)-3-methyltetradecane | C15H32 | 534.2 | 539.5 | 544.9 | 539.572 |
| 16 | (3R)-heptan-3-ol | C7H16O | 424.8 | 429.6 | 434.3 | 429.662 |
| 17 | (3R,4R)-3,4-dimethylheptane | C9H20 | 409.2 | 413.6 | 418.0 | 413.470 |
| 18 | (3R,4S,5S)-3,4,5-trimethylheptane | C10H22 | 431.3 | 436.4 | 441.6 | 436.253 |
| 19 | (3S)-3-methylcyclopent-1-ene | C6H10 | 334.7 | 338.2 | 341.8 | 338.337 |
| 20 | (3Z)-hex-3-ene | C6H12 | 336.2 | 339.6 | 343.0 | 339.663 |
| 21 | (4R)-1-methyl-4-(prop-1-en-2-yl)cyclohex-1-ene | C10H16 | 443.7 | 449.8 | 455.7 | 449.881 |
| 22 | (4R)-4-methyltridecane | C14H30 | 514.5 | 519.6 | 524.8 | 519.834 |
| 23 | (4R,5R)-4,5-dimethyloctane | C10H22 | 430.8 | 435.3 | 439.7 | 435.292 |
| 24 | (4R,6R)-2,4,6-trimethyldecane | C13H28 | 472.3 | 477.0 | 481.8 | 477.197 |
| 25 | (4S)-4-ethenylcyclohex-1-ene | C8H12 | 397.0 | 401.0 | 405.1 | 401.172 |
| 26 | (4S)-4-methyloctadecane | C19H40 | 589.7 | 595.6 | 601.6 | 595.727 |
| 27 | (5R)-5-methyloctadecane | C19H40 | 589.7 | 595.6 | 601.6 | 595.460 |
| 28 | (5R)-5-methyltridecane | C14H30 | 513.0 | 518.1 | 523.3 | 518.032 |
| 29 | (5S)-5-methylhenicosane | C22H46 | 625.8 | 632.1 | 638.5 | 632.008 |
| 30 | (5S)-5-methyltetradecane | C15H32 | 529.6 | 534.9 | 540.3 | 534.845 |
| 31 | (ethylsulfanyl)ethane | C4H10S | 357.6 | 365.0 | 369.4 | 364.692 |
| 32 | [(1E)-2,4-dimethylpent-1-en-1-yl]benzene | C13H18 | 503.9 | 509.0 | 514.1 | 508.748 |
| 33 | 1-(ethylsulfanyl)butane | C6H14S | 412.0 | 417.2 | 421.6 | 416.955 |
| 34 | 1-(prop-2-en-1-yl)cyclohex-1-ene | C9H14 | 423.4 | 430.9 | 437.5 | 430.947 |
| 35 | 1,2-diphenylbenzene | C18H14 | 599.0 | 606.7 | 616.8 | 606.769 |
| 36 | 1,4-dimethylnaphthalene | C12H12 | 535.0 | 540.4 | 545.9 | 540.329 |
| 37 | 1-ethyl-1-methylcyclopentane | C8H16 | 390.7 | 394.7 | 398.7 | 394.401 |
| 38 | 1-ethyl-3-methylbenzene | C9H12 | 427.4 | 434.2 | 438.9 | 434.265 |
| 39 | 1-methylcyclopent-1-ene | C6H10 | 341.7 | 348.5 | 352.7 | 348.602 |
| 40 | 1-tert-butyl-4-ethylbenzene | C12H18 | 474.7 | 484.2 | 492.3 | 484.252 |
| 41 | 2-(methylsulfanyl)propane | C4H10S | 352.6 | 359.1 | 370.9 | 358.861 |
| 42 | 2,2,5-trimethylhexane | C9H20 | 393.2 | 397.3 | 401.3 | 397.280 |
| 43 | 2,2-dimethyldecane | C12H26 | 469.3 | 474.0 | 478.8 | 473.907 |
| 44 | 2,2-dimethylpentadecane | C17H36 | 557.4 | 563.0 | 568.7 | 563.157 |
| 45 | 2,5-dimethylhexa-1,5-diene | C8H14 | 380.4 | 387.5 | 393.1 | 387.423 |
| 46 | 2,6-dimethylheptane | C9H20 | 404.3 | 408.4 | 412.5 | 408.165 |
| 47 | 2,7-dimethyloctane | C10H22 | 428.7 | 433.1 | 437.5 | 432.989 |
| 48 | 2-methylcyclopenta-1,3-diene | C6H8 | 342.4 | 346.0 | 349.7 | 346.242 |
| 49 | 2-methylpent-2-ene | C6H12 | 334.8 | 339.9 | 344.0 | 339.703 |
| 50 | 2-methylprop-2-enal | C4H6O | 337.8 | 343.2 | 350.2 | 343.118 |
| 51 | 2-methylpropane-1,3-diol | C4H10O2 | 480.0 | 486.5 | 492.1 | 486.625 |
| 52 | 3,3-dimethylpentane | C7H16 | 355.6 | 359.3 | 363.0 | 358.978 |
| 53 | 3-ethyl-2-methylpentane | C8H18 | 384.7 | 389.0 | 394.7 | 389.171 |
| 54 | 3-ethyl-3-methylheptane | C10H22 | 432.6 | 437.0 | 441.4 | 436.730 |
| 55 | 3-ethyl-3-methylhexane | C9H20 | 409.6 | 413.8 | 417.9 | 413.709 |
| 56 | 3-ethyl-3-methylpentane | C8H18 | 387.5 | 391.5 | 395.5 | 391.600 |
| 57 | 3-ethyl-5-methylphenol | C9H12O | 500.7 | 507.7 | 514.1 | 507.605 |
| 58 | 3-ethylpyridine | C7H9N | 434.2 | 438.5 | 442.9 | 438.786 |
| 59 | 3-methylbutanoic acid | C5H10O2 | 443.0 | 449.4 | 454.4 | 449.432 |
| 60 | 3-methylbutyl acetate | C7H14O2 | 408.3 | 415.0 | 421.0 | 415.070 |
| 61 | 4-(propan-2-yl)heptane | C10H22 | 427.8 | 432.8 | 437.5 | 432.598 |
| 62 | 4-(propan-2-yl)phenol | C9H12O | 496.0 | 501.2 | 506.4 | 501.061 |
| 63 | 5-ethyl-2-methylpyridine | C8H11N | 444.2 | 451.4 | 457.0 | 451.484 |
| 64 | 5-methyl-1,2,3,4-tetrahydronaphthalene | C11H14 | 502.5 | 507.5 | 512.6 | 507.234 |
| 65 | 5-methylhex-1-yne | C7H12 | 361.4 | 365.0 | 368.7 | 364.842 |
| 66 | 5-methylhexan-2-one | C7H14O | 411.0 | 417.4 | 422.3 | 417.192 |
| 67 | 6-methylhept-1-ene | C8H16 | 381.9 | 386.2 | 390.3 | 386.379 |
| 68 | but-3-enenitrile | C4H5N | 386.3 | 391.7 | 397.1 | 391.630 |
| 69 | butyl octadecanoate | C22H44O2 | 610.0 | 632.9 | 665.8 | 633.035 |
| 70 | decahydronaphthalene | C10H18 | 453.5 | 460.3 | 473.2 | 460.080 |
| 71 | decylbenzene | C16H26 | 560.4 | 571.2 | 578.9 | 571.000 |
| 72 | dimethyl sulfide | C2H6S | 306.1 | 310.4 | 314.3 | 310.506 |
| 73 | ethane-1,2-dithiol | C2H6S2 | 414.0 | 419.2 | 424.4 | 419.257 |
| 74 | ethyl 2-methylprop-2-enoate | C6H10O2 | 386.3 | 390.4 | 395.1 | 390.103 |
| 75 | hept-1-yne | C7H12 | 368.5 | 372.9 | 376.9 | 372.858 |
| 76 | heptan-1-ol | C7H16O | 441.7 | 449.2 | 454.4 | 449.165 |
| 77 | hexadec-1-ene | C16H32 | 541.8 | 558.2 | 576.7 | 558.188 |
| 78 | hexadecylcyclohexane | C22H44 | 646.5 | 653.0 | 659.6 | 653.055 |
| 79 | hexanoic acid | C6H12O2 | 473.2 | 478.7 | 486.5 | 478.700 |
| 80 | hydrazine | H4N2 | 382.3 | 386.7 | 390.9 | 386.409 |
| 81 | hydrogen sulfide | H2S | 208.9 | 212.7 | 215.8 | 212.951 |
| 82 | methyl 3-methoxypropanoate | C5H10O3 | 411.5 | 415.7 | 419.9 | 415.656 |
| 83 | methyl tetradecanoate | C15H30O2 | 564.5 | 570.2 | 575.9 | 569.894 |
| 84 | nona-1,8-diyne | C9H12 | 430.8 | 435.2 | 439.5 | 434.842 |
| 85 | nonanenitrile | C9H17N | 492.2 | 497.2 | 502.2 | 497.252 |
| 86 | nonanoic acid | C9H18O2 | 521.3 | 528.0 | 534.1 | 528.196 |
| 87 | nonylbenzene | C15H24 | 548.2 | 554.9 | 560.8 | 554.678 |
| 88 | oct-1-yne | C8H14 | 394.4 | 399.6 | 405.2 | 399.530 |
| 89 | octacosane | C28H58 | 697.8 | 706.9 | 726.4 | 706.841 |
| 90 | octane-1-thiol | C8H18S | 452.1 | 470.5 | 477.1 | 470.586 |
| 91 | octanenitrile | C8H15N | 473.3 | 478.3 | 483.2 | 478.018 |
| 92 | pent-1-ene | C5H10 | 299.2 | 304.4 | 315.7 | 304.417 |
| 93 | phenyl acetate | C8H8O2 | 460.5 | 467.8 | 473.7 | 467.861 |
| 94 | propan-2-ol | C3H8O | 351.4 | 355.8 | 385.4 | 355.740 |
| 95 | propane-1-thiol | C3H8S | 335.3 | 340.6 | 344.5 | 340.705 |
| 96 | propyl 2-methylpropanoate | C7H14O2 | 402.5 | 407.8 | 412.8 | 407.719 |
| 97 | propyl hexanoate | C9H18O2 | 455.5 | 460.4 | 465.3 | 460.499 |
| 98 | propyl pentanoate | C8H16O2 | 436.2 | 440.7 | 445.1 | 440.592 |
| 99 | thiirane | C2H4S | 322.4 | 327.9 | 332.0 | 327.604 |
| 100 | tris(2-methylpropyl)amine | C12H27N | 464.5 | 469.2 | 473.9 | 469.114 |
上表中给出的预测数据是通过使用基于3D QSPR方法的最终QSQN模型获得的。每个化合物的实验数据不仅有筛选的点,还有值最小和值最大的点。
还有更多的其它常数性质用实验数据验证的例子。查看其它性质案例
对于和温度相关的性质通过绘制性质随温度变化的函数,用实验数据进行了模型验证。已经创建并验证了每种性质1000到10000个2D绘图的订单。举例说明,对癸烷理想气体(C10H22)热容的QSQN模型预测与筛选的实验数据之间的对比如下图所示。
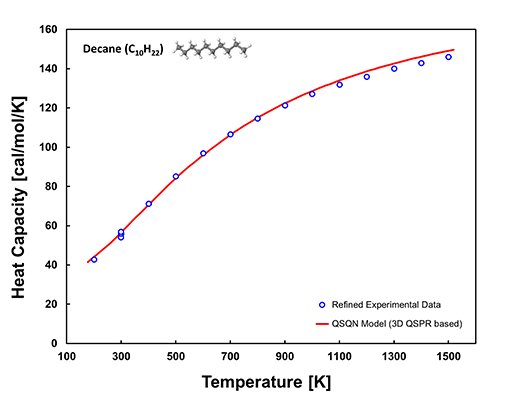
上面2D图中,红线是由基于3D QSPR的QSQN模型生成的,而蓝色圆圈表示筛选的实验数据,模型线与实验点高度一致。
还有更多与温度相关特性的实验数据验证案例。查看更多示例
为了进行比较,我们还验证了现有的其它物性计算方法。Poling等人4概述了已开发的大量性质预测方法。近几十年来,集团贡献法5和QSPR(定量结构-性质关系)6方法尤其受欢迎。其中,我们选择了Joback7和Gani8等众所周知的方法,它们广泛使用在许多工业应用中,包括Aspen Plus9等过程模拟软件。下表总结了所选择和验证的传统方法清单
| Property | Exisitng Approaches |
|---|---|
| Acentric Factor | Gani |
| Critical Compressibility Factor | Joback, Gani |
| Critical Pressure | Joback, Gani |
| Critical Temperature | Joback, Gani |
| Critical Volume | Joback, Gani |
| Enthalpy (Heat) of Formation for Ideal Gas at 298.15 K | Joback, Gani |
| Enthalpy (Heat) of Fusion at Melting Point | Joback |
| Gibbs Energy of Formation for Ideal Gas at 298.15 K and 1 bar | Joback, Gani |
| Heat (Enthalpy) of Vaporization at Normal Boiling Point | Joback |
| Liquid Molar Volume at 298.15 K | Gani |
| Normal Boiling Point | Joback, Gani |
| Heat Capacity of Ideal Gas | Joback |
| Heat Capacity of Liquid | Bondi10 |
| Heat of Vaporization | Watson11 |
| Liquid Density | Rackett12, Gunn-Yamada13 |
| Second Virial Coefficient | Mccann14 |
| Surface Tension | Brock-Bird15, Miller16 |
| Thermal Conductivity of Gas | Misic-Thodos17, Mod-Eucken18 |
| Thermal Conductivity of Liquid | Sato-Riedel19 |
| Vapor Pressure of Liquid | Riedel20 |
| Viscosity of Gas | Reichenberg21 |
| Viscosity of Liquid | Joback, Letsou-Stiel22, Orrick-Erbar23 |
以常沸点为例,Joback和Gani方法预测的常沸点与实验数据的奇偶图和偏差百分比如下所示。
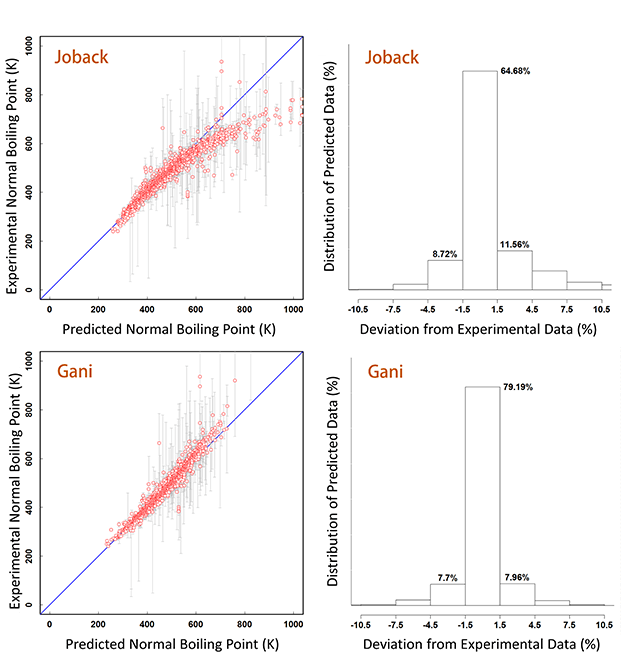
随着沸点的增加,Joback方法的预测值偏低,而Gani方法偏高。用Joback方法,只有64.68%的预测点与筛选实验数据的偏差在1.5%以内,而用Gani方法也只有79.19%。
一般来说,尤其是应用于具有大量重原子和/或多个官能团的复杂化合物时,已知的多数知名方法变得不可靠。可能是由于使用了经验性的公式和/或参数,预测精度经常变得非常低。因此对于较重化合物,其预测数据可能仅作为补充信息以对性质数据的数量级有个概念性认知。
现有预测方法的更多例子查看更多示例
QSQN技术能生成化合物的关键信息,但它需要大量的复杂计算(包括量子化学计算),这些计算一般化学家或化学工程师难以应对。我们自主建立了一个大规模的多核计算系统,提供了尽可能高效的深数据。所有的计算都是预先选定的化合物。然后将结果存储,无需进一步计算而直接提供给用户使用。
该计算系统设计用于自动处理大量化合物,由3个服务器组组成,即管理服务器、文件服务器和计算服务器。管理服务器生成十万到数百万个化合物结构,并在执行构象分析后产生用于量子化学计算的输入文件。然后,管理服务器将量子化学计算任务分发给计算服务器。一旦任何CPU核完成当前计算任务,管理服务器就会自动分配新的计算任务。
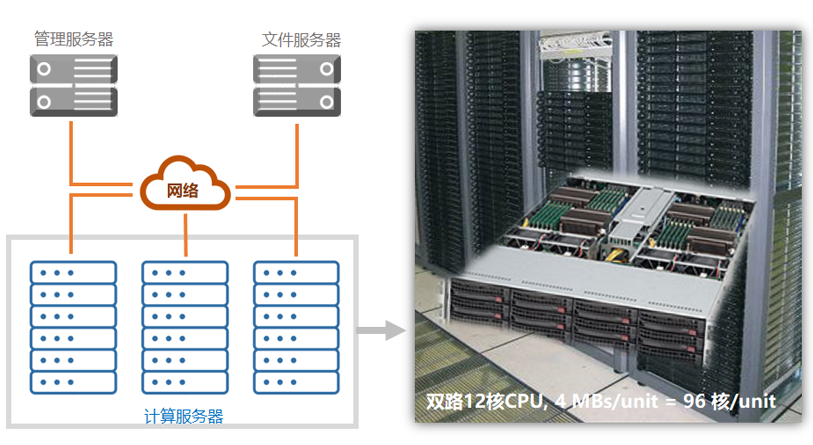
计算服务器执行量子化学计算和分子描述符估算任务,然后使用基于大量核心的QSQN和QN模型来生成性质数据。每个单元包含4个带有双12核CPU的主板(即96个CPU核)用于同时和/或并行执行大规模计算。已经建立了1000多个CPU核来执行大规模计算任务。量子化学计算、分子描述符估算和QSQN/QN模型计算的所有结果都被发送到文件服务器,以便安全存储和备份。
从3D结构生成到最终的深数据产生,整个过程都是自动运行的。这一过程使用了70多个计算机程序模块和软件,它们大多是我们自主开发的。目前,该计算系统每月可以处理约10万个化合物。截至2022年10月,已经计算了400多万个化合物。如果有必要,该系统可以通过简单地添加更多的计算服务器来处理单位周期内更大量的化合物,从而易于扩展。换句话说,通过简单地添加更多的计算服务器,就可以每月处理数百万种化合物,而不只是每月十万种。
所有多核计算过程得到的性质数据都经过系统的检查。首先将QSQN模型(基于3D QSPR)和QN模型(基于2D QSPR)产生的数据与筛选的实验数据和实验数据的范围(如果可用)进行比较。如果产生的数据足够接近筛选的实验数据和/或在实验数据范围内,则认定其满足要求。
实验信息经常不可用,因此将QSQN/QN产生的数据与类似化合物的可用实验数据进行比较。类似的化合物是基于诸如Tanimoto的算法和/或化合物之间的分子描述符的平方相关系数来自动选择的。然后共同分析QSQN/QN产生的数据以及类似化合物的所有可用数据,包括实验信息和现有方法产生的数据。下图显示了检查组件的示例
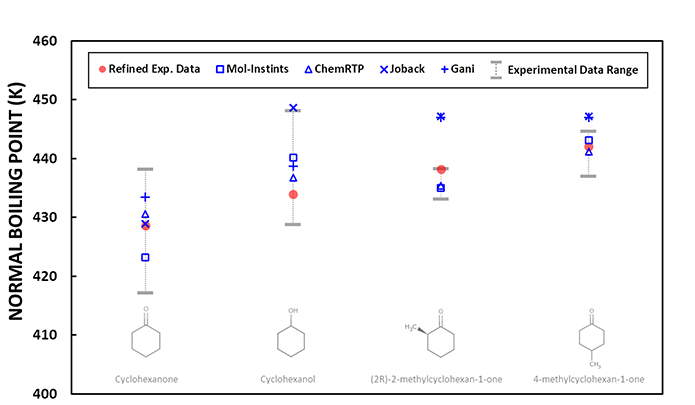
该图显示了支链环己烷的常沸点,实验数据用红圈标记,实验数据的范围用灰色条线标记。在没有4-甲基环己-1-酮(4-methylcyclohexan-1-one)实验信息的情况下,选择了3种类似的化合物,即环己酮(cyclohexanone)、环己醇(cyclohexanol)和(2R)-2-甲基环己-1-酮((2R)-2-methylcyclohexan-1-one),并将它们的实验信息和各类计算的数据绘制在一起。
图表显示,QSQN/QN产生的数据大多与筛选后的实验数据足够接近,并且在3种类似化合物的实验数据范围内,这表明对于支链环己烷化合物的常沸点,QSQN/QN产生的数据基本可靠。图表还显示,在这个案例中,现有方法(即Joback和Gani)生成的数据可以作为补充信息提供良好的初始近似值。对于4-甲基环己烷-1-酮,QSQN/QN产生的数据可以认为是可靠的,因为3个类似化合物的相关数据基本一致,并且现有的方法给出的数据值很接近。
构建了一个数据库系统来存储和提供深数据,这些深数据由大规模多核计算生成并经过数据质量检查。该数据库不仅包含由性质数据、谱学数据、量子化学数据和分子描述符数据组成的深数据,还包括用于对比的通过现有方法确定的一些性质数据。此外还有化学标识符,如InChI、InChIKey、IUPAC名称和同义词,以及基本信息,如2D和3D结构、分子量和化学式等。
利用基于2D QSPR模型的QN技术,构建了一个实时计算系统,该系统提供了超过25个常量性质数据。实时计算系统可以提供任意化合物的数据,而数据库系统只能提供已计算好的化合物数据。
深数据通过两个简单的计划提供,即交付和订阅计划。交付计划根据需求直接向用户发送数据文件(查看数据文件样本),而订阅计划允许用户访问数据库系统和/或实时计算系统以在线获取数据。数据库系统可通过Mol-Instincts网站访问,而用于访问实时计算系统的网络界面为ChemRTP。查看Mol-Instincts样本页 查看ChemRTP样本页